Introduction to Index numbers class 11 notes are presented in this post for easy access to the students. By taking these notes, you can stay active and engaged throughout your reading, revision, and lectures. They also help with clear thinking and understanding. Choose the most important ideas to focus on. These notes provide a useful record of important information and its sources. You’ll be able to recall better what you heard or learnt with these notes.
Index number under Introduction to Index numbers
An index number is a statistical tool for determining the magnitude of changes in a group of related variables. The general trend of diverging ratios from which it is calculated is represented by it.
- “Index numbers are devices for measuring differences in the magnitude of a group of related variables,” Croxton and Cowden stated.
- Index numbers are expressed as percentages.
- Index numbers are a way to measure a group of data in a relative way.
- The quantitative change in the aforementioned variables over time can be precisely measured using index numbers.
- Changes are shown in terms of averages by index numbers.
- They are represented numerically.
- The comparison of studies over various time periods is made easier by the index number.
Features of Index number under Introduction to Index numbers
The various properties of index numbers are as follows:
- Specialised averages are the index numbers: It is possible to compare two or more series using averages like the mean, median, or mode. However, averages cannot be used to compare two or more series if the units in which they are expressed are different or if the items in the series are of different types. Index numbers make it easier to compare changes of series in these situations.
- Percentages are used to represent index numbers: Regardless of the units of measurement, percentages are used to represent the magnitude of the changes in the group. This makes it easier to compare two or more index numbers in a variety of situations. The percentage sign, however, is never used.
- The effect of changes in relation to time or place is measured by index numbers: Changes over time, between locations, and within categories can be compared using index numbers. A city’s cost of living can be compared across two time periods, or the cost of living can be different at the same time in two different locations.
- Index numbers are used to measure changes that cannot be directly measured: The purpose of index numbers is to investigate changes in the effects of factors that cannot be directly measured. The cost of living, for instance, cannot be directly quantified. It can only be studied in terms of its relative changes by looking at how certain other factors that are related to it change.
How to use index numbers under Introduction to Index numbers
Index numbers are frequently used to track changes in output, income, productivity, business activities, and other variables. Variations are measured using index numbers in almost every aspect of economic activity.
- Aids in Policy Development: Any government or non-governmental organisation’s management relies on index numbers. Many policy decisions are based on these trends and tendencies, which aid in the study of various trends of phenomenon. They are also used to plan and create a variety of policies for businesses and the government.
- Economic barometers are index numbers: An instrument that measures atmospheric pressure is called a barometer. Index numbers function as a barometer to detect shifts in a nation’s overall economic conditions and measure the economy’s pulse.
- Aid in analysing trends: When looking at a series and its trend or tendency over time, index numbers are very helpful. They assist in determining the prevailing pattern of exports, imports, industrial production, prices, and a wide range of other phenomena. They also aid in forecasting future trends, which are crucial to the success of any business or production activity in the future. Changes cannot be measured in absolute terms. However, index numbers provide a relative measure of changes in a group of magnitudes of the variables. It is simple to compare the changes over time and in place.
- The purchasing power can be measured using index numbers: The purchasing power of money and the value of money are both dependent on the prices of commodities. The fluctuation in prices has a negative impact on the value of money. The purchasing power of money, or value, decreases when the price level rises. When compared to its purchasing power in 1980, a rupee is said to be worth only 20 paise today. Index numbers are useful for determining a currency’s intrinsic value in comparison to its nominal value. This contributes to the nation’s wage policy formulation.
Limitations of Index numbers
- It only offers relative changes: Index numbers are only estimates of how various events changed relative to one another. Because they are only approximate indicators, they are unable to speak the truth. They are a representation of the generalised truth that is derived from the average of all the items. As a result, it is not applicable to individual units.
- Inadequacy of Accuracy:, Every single thing is not taken into account. The index number will undoubtedly yield an incorrect result if the samples are insufficient or selected in an incorrect manner.
- The distinction between the construction method and its purpose: An index number that was created in a specific way for a specific purpose will not be suitable for all other purposes and situations. It will undoubtedly draw incorrect conclusions if they are utilised for other purposes.
- Ignore changes in quality: The changes in the product’s quality are ignored when calculating the price or production index numbers. An improvement in the product’s quality may result in an increase in price. The index numbers do not reflect such modifications.
- Alterations are conceivable: In order to achieve the desired outcome, index numbers can be constructed in this manner. By selecting a specific base year, a particular group of commodities, a particular set of prices, etc., one can carry out such a manipulation.
Ways to construct index numbers
There are two ways to construct Index numbers;
- Unweighted Index numbers
Since no item is explicitly given a weight in the unweighted index numbers, it is expected that each item has the same weight. The following methods can be used to construct such index numbers:
(i) The simple aggregative method

(il) The Simple Average of Price Relatives Method.

This index is an improvement over the simple aggregative price index because it is not affected by the unit in which prices are quoted.
- Weighted Index numbers
While constructing weighted index numbers, rational weights are assigned to all items or commodities in an explicit manner. Such weights indicate the relative importance of items or commodities included in the calculation of an index.
- Weights, which are perfectly rational for one investigation, may be entirely unsuitable for another. In fact, the decision about the rational weights depends on the purpose of the index number and the nature of the concerned data.
Weighted index numbers can be constructed by two methods:
(i) Weighted Aggregative Method
(i) Weighted Average of Price Relatives Method.
Weighted Aggregative Method
Under this method, weights are assigned to various items and instead of finding the simple aggregate of prices, the weighted aggregate of the prices are obtained.
Some of the important methods of constructing Weighted Aggregative Index are:
- Laspeyre’s Method
- Paasche’s Method
- Fisher’s Ideal Method
Laspeyre’s Method
In 1871, Mr. Laspeyres provided a weighted aggregated index in which the quantities of the commodities in the base year served as weights.
- It helps in answering the question, “How much should the expenditure in the current period be on the same basket of commodities if the expenditure in the base year on it is ₹100?”
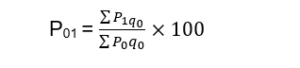
Paasche’s Method
In 1874, the German statistician Paasche created an index number in which quantities in a current year are used to calculate weights.
- It helps to answer the question, “How much should we spend in the current period on the same basket of commodities if the base period basket of commodities was consumed and we spent ₹ 100 on it?”
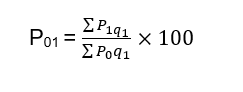
Fischer’s Method
A number of formulas for creating index numbers have been provided by Prof. Irving Fisher; one of these he refers to as the “ideal index.”
The following formula can be used to calculate the Fisher’s Ideal Index:
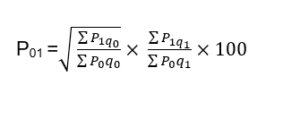
Which is the ideal method among these three?
Fischer’s method is best for calculating index number because;
- The best average for constructing index numbers, the geometric mean, serves as the foundation for the formula;
- It weighs quantities from the base year and the current year. As a result, it avoids the bias that is associated with the Paasche and Laspeyres indexes.
- It passes both the factor reversal test and the time reversal test.
Weighted Average of Price relatives method
In this method, the price relatives for the current year are calculated on the basis of the base year prices. These price relatives are multiplied by the respective weights of the items. These products are added up and divided by the sum of weights.
Steps:
- Calculate, P1/P0 × 100 and denote it by R;
- Multiply the price in the base year (Po) with weights (qo) to get value weights and denote it by W;
- Multiply the price relatives (R) with value weights (W) of each commodity and obtain its total to get sigma RW;
- Obtain the sum total of value weights to get sigma W;
- Apply the formula: Po = ∑RW/∑W
Types of Index Numbers
- The Wholesale Price Index (WPI)
- The Consumer Price Index (CPI), also known as the Cost of Living Index;
- The Industrial Production Index (IIP)
The Consumer Price Index, also known as the Cost of Living Index, is the number that measures the average change in prices paid by a particular class of consumers for the goods and services they consume in the current year compared to the base year. This index is also known as the Cost of Living Index.
Consumer price index – Construction
It includes the following steps;
- Selection of the consumer class
- Information about the family budget
- Choice of base year
- Information about prices
- Weightage – There are two ways to assign weights
- Quantity weight
- Expenditure weight
The following formula is used to calculate the consumer price index:
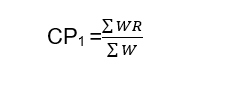
Where,
W = p0 × q0
The Wholesale Price Index (WPI) measures how the prices of commodities traded in wholesale markets have changed over time. The numbers for the wholesale price index are calculated weekly in India.
The changes in the level of industrial production across numerous industries are measured by the industrial production index number.
- It encompasses both public and private sector production.
- It is a relative quantity-weighted average.
Construction of the Index Number of Industrial Production
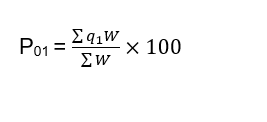
Inflation and Index numbers
A situation characterised by a sustained rise in the overall price level is referred to as inflation. A little ascent in costs or an unpredictable cost rise can’t be called expansion. The term “inflation” refers to a steady and significant rise in prices.
- The most widely used price index to measure the economy’s inflation rate is the Wholesale Price Index (WPI).
- It is the only general index that covers all price changes and shows how commodities’ prices change across all trades and transactions.
- WPI is made available every week with a minimum delay of two weeks.
- WPI is the most widely used inflation measure because of all of these characteristics.
Conclusion
Introduction to Index numbers class 11 notes give a wholesome definition of supply and various related concepts. These notes also provide the factors affecting the price elasticity of demand. You can stay active and engaged throughout your reading, revision, and lectures by taking these notes. Additionally, they aid in clear thinking and comprehension. Selectively identify important ideas. A useful record of important information and its sources can be found in these notes. These notes will help you remember what you heard better.